
我们训练了一个模型,通过对每个正确的推理步骤进行奖励(“过程监督”)来提高解决数学问题的水平,而不是像之前一样只是简单地奖励最终的正确答案(“结果监督”)。
除了提高与结果监督相关的性能外,过程监督在对齐上也有一个非常重要的好处:它能直接训练模型产生被人类认可的思维链。
介绍近年来,大型语言模型在执行复杂的多步推理的能力方面有了很大的提高。然而,即使是最先进的模型仍然会产生逻辑错误,我们通常称为幻觉(hallucinations)。减轻幻觉是构建与人类价值观和道德标准对齐的通用人工智能 AGI (aligned AGI)的关键一步。
其中的 aligned 指的是人工智能的目标与人类价值观和道德准则保持一致或对齐。如果超级智能的目标不一致或不被对齐,可能会有损人类利益,甚至有造成灾难的风险。所以,研究人工智能安全性的专家们提出,在开发高级人工智能和通用人工智能时,需要解决"对齐问题"(aligned problem),确保其目标与人类价值观一致,避免智能系统由于目标不一致而产生的潜在危害。
我们可以通过“结果监督”或“过程监督”的方式训练奖励模型来检测幻觉。“结果监督”根据最终结果提供反馈,“过程监督”为思维链中的每一步提供反馈。在之前的工作[1]的基础上,我们使用MATH数据集[2]作为我们的测试平台,详细地比较了这两种方法。我们发现,即使从结果来判断,过程监督也可以显著提高性能。为鼓励相关研究,我们发布了完整的过程监督数据集。
对齐影响过程监督比结果监督有几个对齐优势。因为过程中的每个步骤都受到精确的监督,它可以直接奖励模型遵循与人类一致的思维链。过程监督也更有可能产生可解释的推理,因为它鼓励模型遵循人类批准的过程。相比之下,结果监督可能会奖励非对齐的过程,而且通常难以审查。
在某些情况下,更安全的人工智能系统方法可能会导致性能下降,这种代价被称为“对齐税”。一般来说,任何对齐税都可能妨碍对齐方法的采用,这是使用最高性能模型所带来的压力。我们下面的结果表明,过程监督实际上会产生负对齐税,至少在数学领域是这样。这可能会让我们考虑更多使用过程监督,我们认为这会产生更积极积极的对齐副作用。
"负对齐税"这个说法的意思是,采用某种方法并没有产生预期的性能损失,反而导致了性能提高。
本节的主要观点是:1) 过程监督相比结果监督有多个对齐优势。2) 过程监督可以直接奖励模型遵循与人类一致的思维链,并且更易产生可解释的推理。3) 结果监督可能奖励非对齐的过程,且难以审查。4) 更安全的人工智能系统方法可能会导致性能下降,这被称为“对齐税”。5) “对齐税”可能阻碍对齐方法的采用,但我们的结果显示过程监督实际产生负对齐税。6) 这可能增加过程监督的采用,并产生积极的对齐副作用。
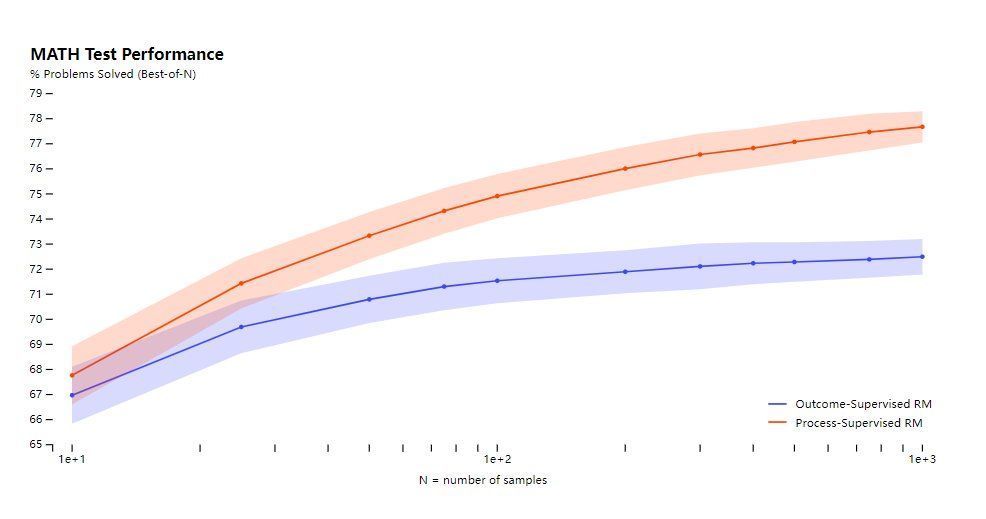
我们使用MATH测试集里面的问题来评估我们的“过程监督”和“结果监督”奖励模型。我们为每个问题生成了许多解答方案,然后选择每个奖励模型排名最高的解答方案。
该图展示了一个函数,即每个奖励模型选择的解答方案数量(number of samples)与选择的解答方案最终能够达到正确结果的百分比(% Problems Solved (Best-of-N))之间的关系。
横轴是选择的解答方案数量,纵轴是正确答案百分比。
过程监督奖励模型不仅在所有方面表现更好,而且随着每个问题解决答案的增多,性能差距会扩大。这表明过程监督奖励模型更可靠。
探索3个类别中的示例:1、真正例子(true positives)2、真负例子(true negatives)3、假正例子(false positives)这三个概念都是机器学习和统计学中的重要指标。真正例子和真负例子都表示判断或检测的准确性,因为两者的判断结果都是正确的。假正例子表示判断的错误,将负例判断为正例,会产生误报。。这三者经常一起使用来评估模型或判断方法的性能,主要指标有:精确率(Precision):真正例子数/(真正例子数+假正例子数),表示正例判断的准确度。召回率(Recall):真正例子数/真实的正例总数,表示找到真实的正例的比例。F1值:2*(精确率*召回率)/(精确率+召回率),综合考虑精确率和召回率。
Open AI 展示了10个数学问题和对应的解决方案,还附上了奖励模型的优缺点评价。这10个数学问题包括化简三角函数、多项式分解、十进制转换、概率问题、平均值计算、数列求值等。
如化简 tan100∘+4sin100∘。
这个困难的三角函数问题需要连续应用几个不太明显的恒等式。大多数解决方案尝试都会失败,因为很难选择哪些恒等式实际上是有用的。虽然GPT-4通常无法解决这个问题(只有0.1%的解决方案尝试能得到正确答案),但奖励模型正确地认识到这个解决方案是有效的。


如多项式分解。
在这里,GPT-4成功执行了一系列复杂的多项式因式分解。第5步中使用Sophie-Germain恒等式是一个重要的步骤,非常富有洞察力。

以及该问题:找到唯一的奇数整数 t,满足0 < t < 23且t + 2 在 modulo 23 意义下为 t 的反元素。
在第7步和第8步中,GPT-4开始进行猜测和检查。这是一个模型可能出现错误判断的常见场景,即断言某个猜测十分成功,而实际上并非如此。但在此例中,奖励模型验证了每一步,并判断这条思维链是正确的。

更多问题可见 OpenAI 论文。
总而言之,
1)结果监督模型容易在复杂的问题上产生错误判断和“幻觉”,它们难以理解问题解决的完整过程。而过程监督模型可以验证每一步思维,确保最终得到正确的解决方案,防止产生错误判断。 2) 在猜测和检查不确定的推理方法中,结果监督模型很难判断某个猜测是否真的“成功”,容易产生判断失误。而过程监督模型可以评估每一步推理的有效性,判断思维链的正确性,避免产生错误判断。 3) 过程监督模型可以鼓励模型学习明确、可解释的推理步骤,而不仅仅是最终结果。这可以使模型得出的解决方案更加可依赖和可信任。
4) 随着问题难度的增加,结果监督模型的判断误差也在增加,其优势减小。而过程监督模型不会出现这一问题,其判断精度更加稳定可靠。 5) 过程监督模型可以发现和纠正结果监督模型难以发现的错误,使模型有效学习到解决复杂问题所需的知识和推理技能。
综上,过程监督模型相比结果监督模型在判断复杂问题上更加准确可靠,可以指导模型学习到解决问题所需的完整知识,而不仅是只有最终的结果,其优势也随问题难度增加而增强。它通过评估每一步推理来发现并纠正错误判断,避免模型产生“幻觉”。
目前尚不清楚这些结果将在多大程度上推广到数学之外的其他领域,我们认为探索过程监督在其他领域的影响对于未来的工作很重要。如果这些结果具有普遍性,我们可能会发现过程监督为我们提供了两全其美的方法——一种比结果监督更高效、更一致的方法。
参考Uesato, J., Kushman N., Kumar R., Song F., Siegel N., Wang L., Creswell A., Irving G. and Higgins, I., 2022. Solving math word problems with process- and outcome-based feedback. arXiv preprint arXiv:2211.14275.↩︎
Hendrycks D., Burns C., Kadavath S., Arora A., Basart S., Tang E., Song D. and Steinhardt J., 2021. Measuring Mathematical Problem Solving With the MATH Dataset. arXiv preprint arXiv:2103.03874.↩︎
Ouyang L., Wu J., Jiang X., Almedia D., Wainwright C.L., Mishkin P., Zhang C., Agarwal S., Slama K., Ray A., Schulman J., Hilton J., Kelton F., Miller L., Simens M., Askell A., Welinder P., Christiano P., Leike J. and Lowe R., 2022. Training language models to follow instructions with human feedback. arXiv preprint arXiv:2203.02155.↩︎
作者Karl Cobbe;Hunter Lightman;Vineet Kosaraju;Yura Burda;Harri Edwards;Jan Leike;Ilya Sutskever;
致谢贡献者们:Bowen Baker, Teddy Lee, John Schulman, Greg Brockman, Kendra Rimbach, Hannah Wong, Thomas Degry
本文经授权转载「图灵社区」,如需转载,请联系他们的工作人员。
